Basics of Curves

Curve is a line of which no part is straight and which changes direction without angles

• Necessarily evil

• Positive impediments for higher speeds

• Necessity arises due to physical and geographical features.

Curve Designation

• Curves are designated by their radii except on IR and US rail roads

• On IR degree of curve for designation

• Radii for calculation

Degree of Curve

Degree of curve is the angle subtended by 30.5 m chord

On IR the curves are measured by versines-which is mid chord offset on 20 m chord

CURVE EFFECT

• Vehicle running at a speed of V in a curve of radius R experiences a 

    centrifugal force = MV²/R

• Undesirable effects

– Possible passenger discomfort

– Possible displacement of loads

– Risk of vehicle overturning

– Risk of derailment

– High lateral force resulting in

• Curve resistance

• Wear of rail and wheel flange

• Lateral force on track

SUPERELEVATION / CANT

• The effect of centrifugal force is eliminated/reduced by raising the outer rail by a specified amount.

• This raising of outer rail over inner rail is called Superelevation/cant 

C = GV²/127R

Where C is cant / superelevation in mm. G is the gauge of track + width of rail headin mm. R is the radius of the curve in metres.

VEHICLE ON CANTED TRACK

PARAMETERS OF CURVE

• Equilibrium cant Ce / Equilibrium speed ‘Ve’

• Actual cant ‘Ca’

• Cant deficiency ‘Cd’

• Cant excess ‘Cex’

• Rate of change of actual cant ‘RCa’

• Rate of change of cant deficiency ‘RCd’

• Length of transition ‘L’

EQUILIBRIUM CANT

During circular motion, the resultant of weight and centrifugal force is perpendicular to the plane of rail and passes through the centre of track,the corresponding speed is called equilibrium speed and the cant is called equilibrium cant.

EQUILIBRIUM SPEED IS TO BE DECIDED BY CE CONSIDERING 

1.Max. speeds of fast and slow moving 

2.trains Stopping places

3.Permanent speed restriction

4.Junctions

5.Gradient affecting speed of goods train

ACTUAL CANT (Ca)

• Maintenance criteria

– High cant will cause rolling of ballast and flattening of inner rail

– Not very sensitive to wind force

• Safety against derailment

– Empty wagon stopped and started

• Comfort criteria

– No appreciable discomfort upto 180 mm

• Limited to 1/8 to 1/10 of dynamic gauge.

MAXIMUM VALUES OF CANT

CANT DEFICIENCY (Cd):-Train travelling on curve with speed greater than equilibrium speed experience the cant deficiency

• Safety - Upto 175 mm safe with critical wind velocity

• Comfort criteria

– Discomfort if unbalanced lateral acceleration is greater than 0.1g

– Cant deficiency should be less than 0.1g

• Observed value of unbalanced lateral acceleration is more than theoretical value

CANT EXCESS (Cex) :-Train travelling on curve with speed lesser than equilibrium speed experience the cant deficiency

• No comfort consideration

• Maintenance consideration

– Excess wear on inner rail

– More the volume of goods traffic lesser would be cant excess

Maximum Value of ‘C ex’-75 mm on IR’

TRANSITION CURVE

Transition curve is an easement curve introduced between straight and curved track to facilitate gradual change of versine and super elevation.

On IR it is generally laid in shape of cubic parabola

Y = X³/6RL

LENGTH OF TRANSITION CURVE

• Comfort criteria

– Rate of change of ULA less than 0.03g

– Rate of change of Cd <0.03g

– Rate of change of Ca is just noticeable at 65 to 75mm/sec but fixed as

35 mm /sec

– Under exceptional circumstances it can be increased to 55 mm /sec

• Safety criteria

– Cant gradient causes track twist.

– Cant gradient 1in 720 i.e. 1.4 mm/m

– In exceptional cases it can be 1in 360 i.e. 2.8 mm/m

Desirable length of transition will be maximum of

• L =0.008 Ca*Vm

• L =0.008 Cd*Vm

• L =0.72 Ca

Minimum length of transition is given by 2/3rd of maximum value calculated by

above formulae.

SHIFTING OF TRANSITION CURVE

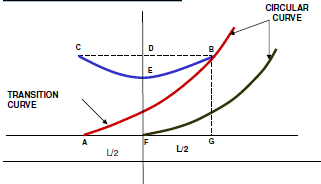
Shift – Main circular arc is moved inward to accommodate with a transition curve laid as cubic parabola by an amount called shift .It is given by S = L²/24R

VIRTUAL TRANSITION -- It is a determined length to facilitate the running out of cant on either side of tangent point when circular curve is directly connected to tangent track .

• For BG- 14.6 M(7.3m on either side of tangent point)

• For MG-13.7 M(6.85m on either side of tangent point)

COMPOUND AND REVERSE CURVE

• Common Transition

• For Compound Curves: Length of transition will be MAX. of

• L =0.008 (Ca1-Ca2)*Vm

• L =0.008 (Cd1-Cd2)*Vm

• L =0.72 (Ca1-Ca2)

• If length is coming less than virtual transition then common transition is deleted and the cant is run out on the length of virtual transition

• For Reverse Curve: Length of transition will be MAX. of

• L =0.008 (Ca1+Ca2)*Vm

• L =0.008 (Cd1+Cd2)*Vm

• L =0.72 (Ca1+Ca2)

REVERSE CURVE

• For high speeds in Group A and B routes a straight of 50m length shall be kept

• Otherwise increase the transition length to eliminate the straight

• If neither of the above two are possible than speed restriction of 130 KMPH on

BG and 100 KMPH on MG

VERTICAL CURVES

• Vertical curves are provided at those locations where algebraic difference

between the grades is equal to or more than 0.4% (4 mm/m)

COMPENSATION FOR CURVATURE ON GRADIENT

• Compensation allowed on gradients due to curvature

– 0.04% per degree for B.G. track

– 0.03% per degree for M.G. track

– 0.02% per degree for N.G. track

Example- calculate the grade compensation to be given for a BG curve of 3º on gradient of 1 in 100.

Solution- total compensation  = 0.04 x 3 %

                                                = 0.12%

Compensated grade                = 1% - 0.12%

                                                = 0.88%

                                                = 1/113.6 say 1/114 Ans.

Lean = H*Ca / G

Sway = H*Ca / 4G

• Inside ----- ¼ of lean due to super-elevation

• Outside ---- Nil

ADDITIONAL CLEARANCE ON CURVE

EXTRA CLEARANCE DUE TO CURVATURE

• Platforms/ Structures

Inside of curve                                -- (Vо+l+S-51)

Outside of curve                              -- (Vе-25)mm

• Between adjacent track                 -- Vо+ Vе+2*(L/4)

Vо = overthrow = C² / 8R,              Vе = endthrow = (L² - C²) / 8R ,

S = sway = ¼th of                           lean l=lean

CHECK RAIL ON CURVES

• On curves of 8 degrees& above

• Min. clearance = 44 mm clearance = 44+ half the gauge widening Safe Speed On Curves – (1) Fully transitioned curves – The maximum permissible speed for transitioned curves should be determined from the following formulae –

___________

(a) BROAD GAUGE –            V = 0.27 √ R (Ca + Cd)

This is on the assumption that the centre to centre distance between railheads is 1750 mm.) ___________

(b) METRE GAUGE –            V = 0.347 √ R (Ca + Cd)

(This is on the assumption that the c/c distance between railheads is 1057 mm.) 

(c) NARROW GAUGE (762 mm.)             – V = 3.65√ (R-6)

Subject to maximum of 50 Kmph

V = speed in Kmph R = radius in metres. 

Ca = Actual cant in mm.

Cd = permissible cant deficiency in mm.

(2) (a) Non transitioned curves with cant on virtual transition –

The determination of the maximum permissible speed on curves without transition involves the concept of the virtual transition. The change in the motion of a vehicle from straight to curve conditions takes place over the distance between the bogie centres, commencing on the straight at half the distance before the tangent point and terminating on the curve at the same half distance beyond the tangent point. Normally, the length of virtual transition is taken as 14.6 meter on B G, 13.7 meter on M G and 10.3 meter on N G. The cant or superelevation is gained over the virtual transition. The cant gradient in any case should not be steeper than 1 in 360 (2.8 mm. per meter) on B.G. and 1 in 720 (1.4 mm. per meter) on M. G. and N. G.

(b) Non-transitioned curves with no cant provided –

In case of non-transitioned curves where no cant is provided, the safe speed over the curve can be worked out from the graph. 

(3) For curves laid with inadequate length of transition, the safe permissible speed should be worked out on the basis of actual cant/cant deficiency, which can be provided taking into consideration the limiting values of cant/cant deficiency

gradient and the rate of change of cant and cant deficiency.

(4) The speed as determined above shall not exceed the maximum permissible speed of the section.

Cuttings of rails on curves: – 

Rails are usually laid with square joints on curve. On curved track the inner rail joints gradually lead over the outer rail joints. When the inner rail of the curve is ahead of the outer rail by an amount equal to half the pitch of bolt holes, cut rails should be provided to obtain square joints. Cut rail is a rail which is shorter than the standard length of rail by an amount equal to the pitch of the bolt holes. The excess length ‘d’ by which the inner rail gains over the outer rail is calculated by the 

 formula –d=LG / R

where ‘d’ is the length in mm. by which the inner rail joint is ahead of the outer rail joint over the entire length of the curve, if cut rails are not provided.

L = length of the curve in meters R= radius of the curve in meters

G= the gauge + width of the rail head in mm.

The number of cut rails for a particular curve is worked out by the formula –

                            N = d / pitch of the bolt holes in mm

It must be ensured that rail joints are square at beginning and at the end of the curve.

Curve board – A curve board is provided on outside of curve showing radius , length of curve , transition length in metre and cant in mm.

Rail post :- It is provided at tangent point on inside of curve at the beginning and end of transition of curve. Painted in red and white.